阿衡的探秘地圖

　　《海島算經》為中國古代數學家劉徽的傑出作品。利用勾股形（直角三角形）的比率算法原理，使用矩（彎曲成直角的尺）、表（垂直入地的量杆）等測量工具創造出「重差術」。《海島算經》使古代中國的測量學方法達到完善與巔峰，並廣為運用在地圖繪製技術的理論發展，曾有美國數學家讚譽「中國在測量學的成就上超越了西方一千年」，貢獻非常卓越。

【《海島算經》第一頁（清乾隆《四庫全書》版本）】

　　劉徽（約西元225～295年），三國時代魏晉數學家，據說是山東淄博淄川人。據《隋書‧律歷志》記載，《九章算術》原共九卷，西元263年劉徽為其作注，並延續了第九卷「勾股章」內容，加入自己的作品《九章重差圖》作為第十卷，直到唐代李淳風把第十卷從《九章算術》中獨立分出成書，按第一問首句「今有望海島」而取名為《海島算經》。現傳的《海島算經》是清乾隆時代所編輯《四庫全書》版本。

【劉徽（中國郵政郵票）】

　　劉徽自幼即習《九章算術》，長大後又繼續深入研究，以「率」思想發展了相似勾股形對應比例關係，以「出入相補、以盈補虛」原理證明了勾股定理並計算面積和體積，其卓越成就受後人重視。宋徽宗時代為恢複數學教學制度，便追封了歷代天算家與數學家，劉徽為其中之一。

　　劉徽《九章算術》注自序中說：「輒造重差，并為注解，以究古人之意，綴於勾股之下。」說明了重差術之精隨乃「相似勾股形對應邊成比例」，此即為相似直角三角形的比例原理，雖然現在來看這不是什麼深奧的數學，但其操作容易，尤其運用多次測望法技巧，創意十足。「凡望極高、測絕深而兼知其遠者必用重差、勾股，則必以重差為率，故曰重差也。」利用表尺重複從不同位置測望，取測量所得的差數進行計算求得山高或谷深，這就是劉徽的重差理論。以下從第一問「望海島」開始解題。

【窺望海島之圖】

第一問　望海島

　　今有望海島，立兩表齊，高三丈，前後相去千步，令後表與前表相直。從前表卻行一百二十三步，人目著地取望島峰，與表末參合。從後表卻行一百二十七步，人目著地取望島峰，亦與表末參合。問島高及去表各幾何？答曰：島高四里五十五步；去表一百二里一百五十步。術曰：以表高乘表間為實；相多為法。除之，所得加表高，即得島高。求前表去島遠近者：以前表卻行乘表間為實；相多為法。除之，得島去表數。

　　題意圖示今有望海島，立兩表AB、CD皆高3丈，彼此前後距離BD為1000步與海島共線。從前表卻行BE為123步，E為人眼貼地望表杆頂和島上山頂對齊之處。從後表卻行DF為127步，F亦為人眼貼地望表杆頂和島上山頂對齊之處。請問島高GH、去表BH各為多少？其中原文「為實」為分子，「為法」為分母。由相似直角三角形關係：

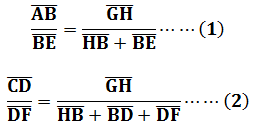
　　因為AB＝CD：

　　把上式帶入（1）式：

　　長度單位之換算有1里＝180丈，1丈＝10尺，1步＝6尺。計算：

　　故得證明與結果，本問論述了「重表法」，運用兩次測望法求出「相多」（兩表卻行之差）代入公式，運用重差，即可得到無法直接去測量的島高和島距離！

第二問　望松生山上

　　今有望松生山上，不知高下。立兩表齊，高二丈，前後相去五十步，令後表與前表參相直。從前表卻行七步四尺，薄地遙望松末，與表端參合。又望松本，入表二尺八寸。复從後表卻行八步五尺，薄地遙望松末，亦與表端參合。問松高及山去表各幾何？答曰：松高一十二丈二尺八寸；山去表一里二十八步、七分步之四。術曰：以入表乘表間為實。相多為法，除之。加入表，即得松高。求表去山遠近者：置表間，以前表卻行乘之為實。相多為法，除之，得山去表。

　　題意圖示今有望松生山上，立兩表AB、CD皆高2丈，彼此前後距離BD為50步與松共線。從前表卻行BE為7步4尺，E為人眼貼地望表杆頂和山上松頂對齊之處，又望松底再得入表AG為2尺8寸。從後表卻行DF為8步5尺，F亦為人眼貼地望表杆頂和山上松頂對齊之處。請問松高HJ、去表BK各為多少？由相似直角三角形關係：

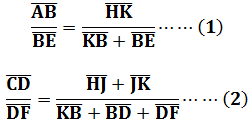
　　由（1）、（2）從第一問之重差法可得：

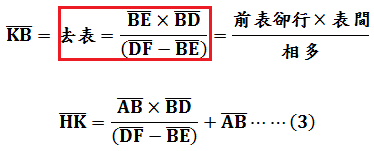
　　又有直角三角形股高比例關係：

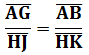
　　代入（3）式：

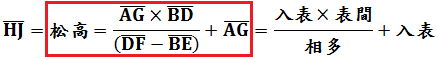
　　長度單位之換算有1里＝180丈，1丈＝10尺，1步＝6尺，1尺＝10寸。計算：

　　本問為三次測望法之應用。

第三問　南望方邑

　　今有南望方邑，不知大小。立兩表東、西去六丈，齊人目，以索連之。令東表與邑東南隅及東北隅參相直。當東表之北卻行五步，遙望邑西北隅，入索東端二丈二尺六寸半。又卻北行去表一十三步二尺，遙望邑西北隅，適與西表相參合。問邑方及邑去表各幾何？答曰：邑方三里四十三步、四分步之三；邑去表四里四十五步。術曰：以入索乘後去表，以兩表相去除之，所得為景差；以前去表減之，不盡以為法。置後去表，以前去表減之，余以乘入索為實。實如法而一，得邑方。求去表遠近者：置後去表，以景差減之，余以乘前去表為實。實如法而一，得邑去表。

　　題意圖示今有南望方邑，東西立兩表以繩連索AB相距6丈，東表A與邑東面城牆F共線。東表之北卻行AC為5步，望邑西北隅G入繩索東端2丈2尺6.5寸。又卻北行去表AD為13步2尺，D為望西表和邑西北隅G對齊之處。請問邑方FG、邑去表AF各為多少？本問為第一問「望海島」之延伸應用，假想有PQ平行AB且等於AE，由相似直角三角形關係：

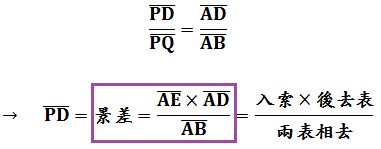
　　長度單位之換算有1里＝180丈，1丈＝10尺，1步＝6尺，1尺＝10寸。計算：

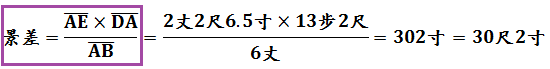
　　從原圖衍生出上圖，應用第一問「望海島」望海島之基本題型，其中，景差－前去表＝不盡：

　　長度單位之換算有1里＝180丈，1丈＝10尺，1步＝6尺，1尺＝10寸。計算：

　　本問論述了「連索法」，運用兩次測望並假想一「後表」求出其「景差」，再運用重差原理，即可得到遠處的邑方和邑去表！

第四問　望深谷

　　今有望深谷，偃矩岸上，令勾高六尺。從勺端望谷底，入下股九尺一寸。又設重矩于上，其矩間相去三丈。更從勺端望谷底，入上股八尺五寸。問谷深幾何？答曰：四十一丈九尺。術曰：置矩間，以上股乘之，為實。上、下股相減，余為法，除之。所得以勾高減之，即得谷深。

　　題意圖示今有望深谷，立一矩在谷邊，矩勾高AB為6尺，從勺端B望谷底G得下股AC為9尺1寸。又重新上移設矩位置，其與原矩間之距離AD為3丈，從勺端E望谷底G得上股DF為8尺5寸。請問谷深AH為多少？本問為利用長方形之對角線面積關係，首先由原圖衍生出下圖：

　　由「相似勾股形對應邊成比例」來觀察以EG為對角線的長方形，紅１、２小長方形之面積互為相等：

　　同理觀察以BG為對角線的長方形，綠３、４小長方形之面積亦互為相等：

　　因為AB＝DE，由面積關係明顯可觀察出：

　　所以：

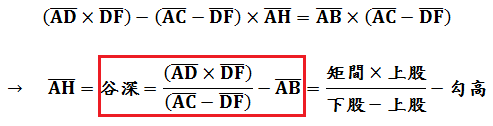
　　長度單位之換算有1丈＝10尺，1步＝6尺，1尺＝10寸。計算：

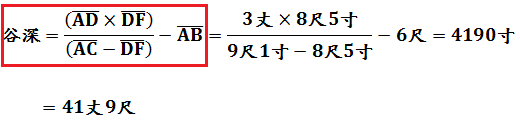
　　本問論述了「累矩法」，運用兩次測望並以「相似勾股形對應邊成比例」，觀察面積關係，即可得到無法下探測量的谷深！

第五問　登山望樓

　　今有登山望樓，樓在平地。偃矩山上，令勾高六尺。從勾端斜望樓足，入下股一丈二尺。又設重矩於上，令其間相去三丈。更從勾端斜望樓足，入上股一丈一尺四寸。又立小表於入股之會，复從勾端斜望樓岑端，入小表八寸。問樓高幾何？答曰：八丈。術曰：上、下股相減，余為法；置矩間，以下股乘之，如勾高而一。所得，以入小表乘之，為實。實如法而一，即是樓高。

　　題意圖示今有登山望樓，樓建於平地，上山矩勾高AB為6尺，從勺端B望樓足G得下股AC為1丈2尺。又重新上移設矩位置，其與原矩間之距離AD為3丈，從勺端E望樓足G得上股DF為1丈1尺4寸。又立小表於F從勺端B望樓頂H再得入小表FJ為8寸。請問樓高GH為多少？本問為第四問「望谷深」之應用，首先由原圖衍生出下圖：

　　由「相似勾股形對應邊成比例」分別來觀察以EG和EH為對角線的長方形中之面積關係：

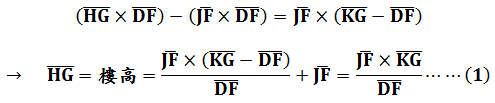
　　其中有直角三角形相似關係：

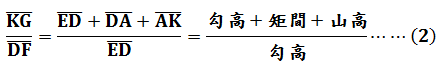
　　由第四問之谷深公式且ED＝BA：

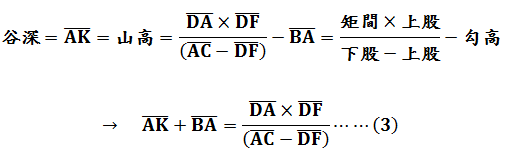
　　綜合（1）、（2）、（3）式得到：

　　長度單位之換算有1丈＝10尺，1尺＝10寸。計算：

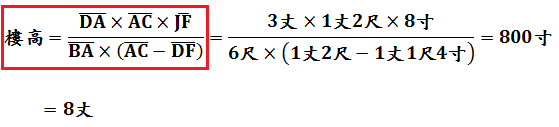
第六問　東南望波口

　　今有東南望波口，立兩表南、北相去九丈，以索薄地連之。當北表之西卻行去表六丈，薄地遙望波口南岸，入索北端四丈二寸。以望北岸，入前所望表里一丈二尺。又卻行，後去表一十三丈五尺。薄地遙望波口南岸，與南表參合。問波口廣幾何？答曰：一里二百步。術曰：以後去表乘入索，如表相去而一。所得，以前去表減之，余以為法；复以前去表減後去表，余以乘入所望表里為實，實如法而一，得波口廣。

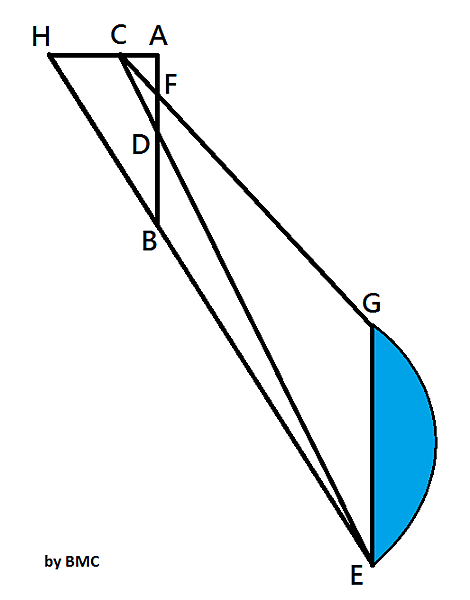
　　題意圖示今有東南望波口，立兩表A、B於南北方位相距9丈，用繩索貼地連起。從北表A往西6丈時，貼地遙望波口南岸E得入索北端AD為4丈2尺，遙望波口北岸G得入前所望表里DF為1丈2尺。再繼續向西行，從H望E與南表B共線時，得AH為13丈5尺。請問波口廣GH為多少？本問為第二問「望松生山上」之應用，首先由原圖衍生出下圖，假想有KJ平行DA且等於DA：

　　套入第二問中的松高公式：

　　由直角三角形相似關係：

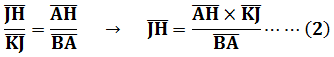
　　將（2）式帶入（1）式且KJ＝DA得到：

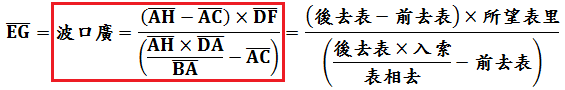
　　長度單位之換算有1里＝180丈，1丈＝10尺，1步＝6尺，1尺＝10寸。計算：

第七問　望清淵下有白石

　　今有望清淵下有白石。偃矩岸上，令勾高三尺。斜望水岸，入下股四尺五寸。望白石，入下股二尺四寸。又設重矩於上，其間相去四尺。更從勾端斜望水岸，入上股四尺。以望白石，入上股二尺二寸。問水深幾何？答曰：一丈二尺。術曰：置望水上、下股相減，余以乘望石上股為上率。又以望石上、下股相減，余以乘望水上股為下率。兩率相減，余以乘矩間為實；以二差相乘為法。實如法而一，得水深。

　　題意圖示今有望清淵下有白石A，立矩於岸上勾高BC為3尺。斜望水岸E處入下股BF為4尺5寸，望白石A入下股BG為2尺4寸。又重新上移設矩位置，其與原矩間之距離BH為4尺，再斜望水岸E處入上股HK為4尺，望白石A入上股HM為2尺2寸。請問水深AE為多少？本問為第四問「望谷深」之應用，套入谷深公式：

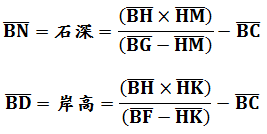
　　由石深－岸高＝水深：

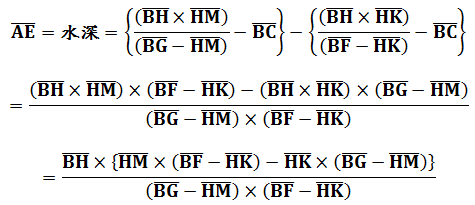
　　其中

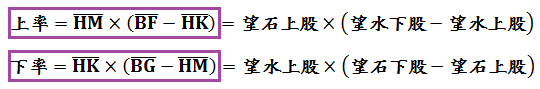
　　長度單位之換算有1丈＝10尺，1尺＝10寸。計算：

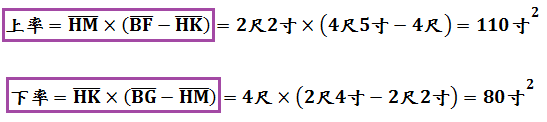
　　本問為四次測望法之應用。另外，本問並未考慮折射現象。因水有折射，則望清淵下白石的實際深度應比看到的還要深。水的折射率為1.33，實際白石水深為：

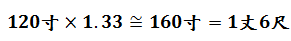
第八問　登山望津

　　今有登山望津，津在山南。偃矩山上，令勾高一丈二尺。從勾端斜望津南岸，入下股二丈三尺一寸。又望津北岸，入前望股里一丈八寸。更登高岩，北卻行二十二步，上登五十一步，偃矩山上。更從勾端斜望津南岸，入上股二丈二尺。問津廣幾何？答曰：二里一百二步。術曰：以勾高乘下股，如上股而一。所得以勾高減之，余為法；置北行，以勾高乘之，如上股而一。所得以減上登，余以乘入股里為實。實如法而一，即得津廣。

　　題意圖示今有登山望津（渡口），津在山的南方，帶矩上山，勾高AB為1丈2尺。從勾端B斜望津南岸C得下股AD為2丈3尺1寸，又望津北岸E得入股里DF為1丈8寸。然後繼續上岩登高，北卻行AG為22步，上登GH為51步，再重新設矩在H位置。從勾端J斜望津南岸C得上股HK為2丈2尺。請問津廣CE為多少？本問為第二問「望松生山上」之應用，首先由原圖衍生出下圖，假想有NO平行AD且等於AD：

　　套入第二問中的松高公式：

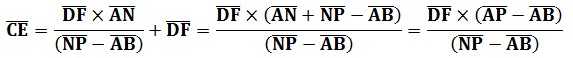
　　其中，利用RH為共餘：

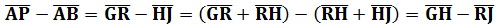
　　所以

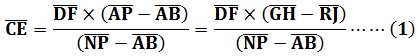
　　由直角三角形相似關係：

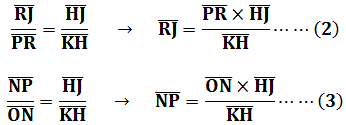
　　將（2）、（3）式帶入（1）式且ON＝DA，PR＝AG得到：

　　長度單位之換算有1里＝180丈，1丈＝10尺，1步＝6尺，1尺＝10寸。計算：

第九問　登山臨邑

　　今有登山臨邑，邑在山南。偃矩山上，令勾高三尺五寸。令勾端與邑東南隅及東北隅參相直。從勾端遙望東北隅，入下股一丈二尺。又施橫勾於入股之會，從立勾端望西北隅，入橫勾五尺。望東南隅，入下股一丈八尺。又設重矩於上，令矩間相去四丈。更從立勾端望東南隅，入上股一丈七尺五寸。問邑廣長各幾何？答曰：南北長一里百步；東西廣一里三十三步、少半步。術曰：以勾高乘東南隅入下股，如上股而一，所得減勾高，余為法；以東北隅下股減東南隅下股，余以乘矩間為實。實如法而一，得邑南北長也。求邑廣：以入橫勾乘矩間為實。實如法而一，即得邑東西廣。

　　題意圖示今有登山臨邑，邑在山的南方，帶矩上山，勾高AB為3尺5寸。令勾端B、東南隅C、東北隅D共面，從勾端B遙望東北隅D得下股AE為1丈2尺。又放置橫勾在E，從立勾端B望西北隅F的入橫勾EG為5尺。望東南隅C的下股AH為1丈8尺。又重新上移設矩在J位置，矩間AJ為4丈。再從立勾端K望東南隅C得上股JM為1丈7尺5寸。請問邑廣DF和邑長CD各為多少？本問為第二問「望松生山上」與第四問「望深谷」之應用。

　　第一步驟，從原圖衍生出第二問「望松生山上」的基本圖型：

　　由「相似勾股形對應邊成比例」分別來觀察以BC和BD為對角線的長方形中之面積關係：

　　第二步驟，從原圖套入第四問中的谷深公式：

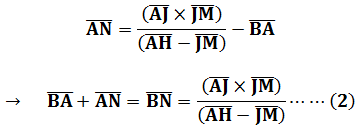
　　將（2）式代入（1）式且得到：

　　第三步驟，由直角三角形相似關係：

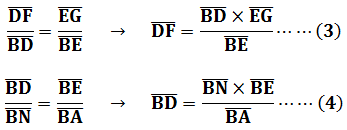
　　將（2）式代入（4）式，再代入（3）式得到：

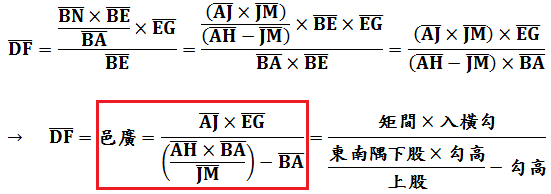
　　長度單位之換算有1里＝180丈，1丈＝10尺，1步＝6尺，1尺＝10寸。計算：

　　本問應用松高公式和谷深公式，頗為複雜，其立體結構和解題思維令人驚艷！