阿衡的探秘地圖

Physics derive: OB Tsai　Write & Edit: BMC

　The study of the motion is an ancient one, making Classical Mechanics one of the oldest and largest subjects in physics. It is also widely known as Newtonian Mechanics. The initial development of Classical Mechanics is often referred to as Newtonian Mechanics, with the mathematical methods invented by Isaac Newton. The most famous equation is known as Newton's Second Law of Motion.

【Isaac Newton（1643－1727）】

　After Newton, more abstract and general methods were developed, leading to reformulations of Classical Mechanics known as Lagrangian Mechanics and Hamiltonian Mechanics. Joseph Lagrange and William Hamilton extend substantially beyond Newton's work, particularly through their use of analytical mechanics.

　Using mathematical analysis and a function called the Lagrangian, choosing the generalized coordinates, with Principle of Least Action, Lagrangian Mechanics is a reformulation of Classical Mechanics. It is widely used to solve mechanical problems when Newton's formulation of Classical Mechanics is not convenient.

【Joseph Lagrange（1736－1813）】

　Hamiltonian Mechanics is also a theory developed from Classical Mechanics. Based on Lagrangian Mechanics, Hamilton uses a different mathematical formalism, providing a more abstract understanding of the theory. It was an important reformulation of Classical Mechanics, which later contributed to the formulation of Statistical Mechanics and Quantum Mechanics.

【William Hamilton（1805－1865）】

　Classical Mechanics and Quantum Mechanics are the two major sub-fields of mechanics. With Wave-particle Duality, Quantum Mechanics use a mathematical way, the wave function, to provide information about the probability amplitude of position, momentum, and other physical properties of a particle. Erwin Schrödinger developed the fundament of Quantum Mechanics and formulated his Schrödinger Equation that describes how the quantum state of a quantum system changes with time. In the Copenhagen Interpretation, the wave function is the most complete description that can be given of Quantum Mechanics' system. Solutions to Schrödinger's Equation describe not only molecular, atomic, and subatomic systems, but also macroscopic systems, possibly even the whole universe.

【Erwin Schrödinger（1887－1961）】

　With Pierre de Fermat's principle of light, Leonhard Euler's mathematical method, Christiaan Huygens' theory of wave source, and Richard Feynman's guess, now we will try to show how finally Schrödinger Equation can be derived from Newtonian Mechanics, during Lagrangian and Hamiltonian, after Wave-particle Duality of Quantum Physics.

Chapter 1－Lagrangian Mechanics

　From Newton's Second Law of Motion

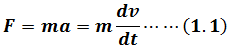
　And Conservative Force is

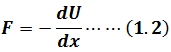
　Let（1.1）＝（1.2）

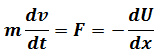
　LHS

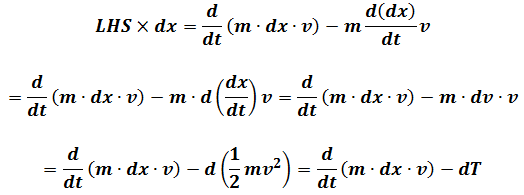
　RHS

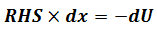
　LHS＝RHS

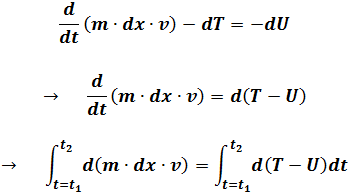
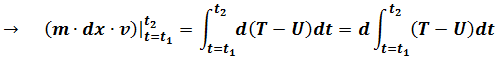
　Define Lagrangian

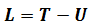
　Action

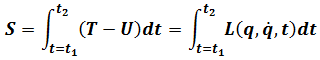
　Principle of Least Action

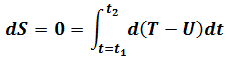
　Also define

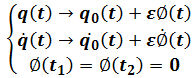
　And

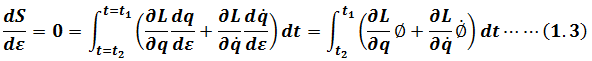
　Here using integration by parts

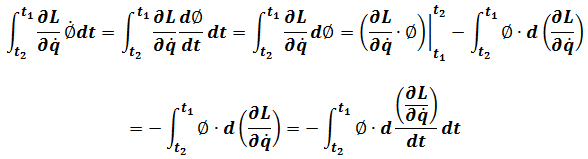
　So（1.3）becomes

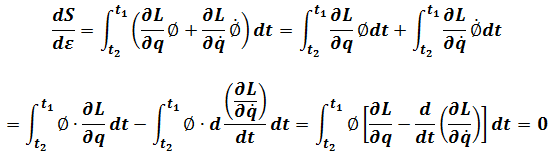
　We get Lagrange's Equations of the first kind

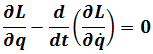
Chapter 2－Hamiltonian Mechanics

　From Newtonian Mechanics

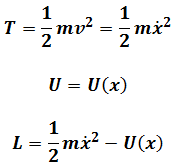
　Partial differential of Lagrangian is

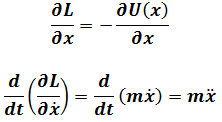
　Where

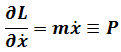
　With spatial translation invariance

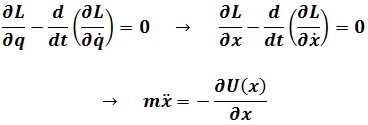
　And time translation invariance

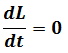
　Here

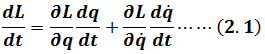
　And

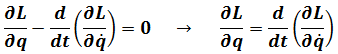
　So（2.1）becomes

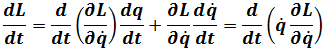
　Now define Hamiltonian

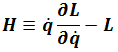
　Where

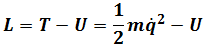
　We get Hamiltonian Energy

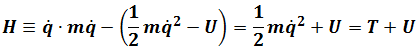
Chapter 3－Partial Differential between Lagrangian and Hamiltonian

　From Lagrangian

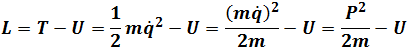
　Here

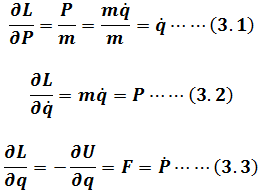
　With partial differential of Lagrangian

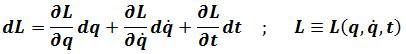
　Taking（3.1）、（3.2）、（3.3）into following formula

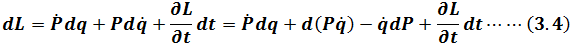
　Where

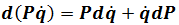
　Minus（3.4）and plus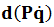   

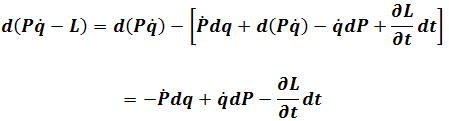
　Come to Hamiltonian

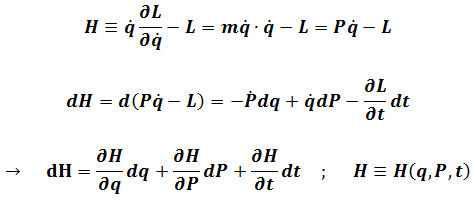
　Where

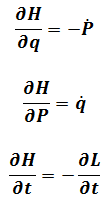
　Then come back to

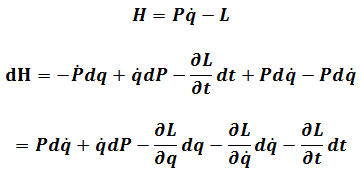
　Where

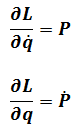
　Because of

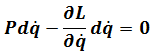
　And

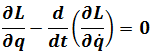
　Here

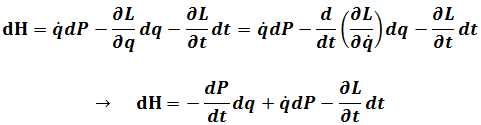
　And

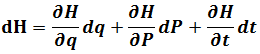
　So

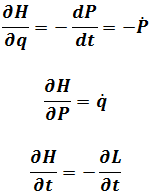
Chapter 4－Hamiltonian Energy with Action

　Considering about

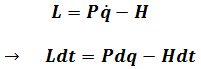
　Action

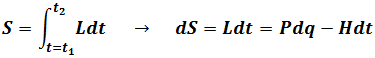
　And

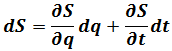
　So

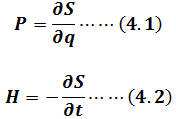
　Hamiltonian Energy is

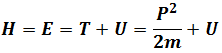
　Taking into（4.1）、（4.2）we get

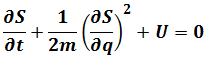
Chapter 5－Derivation of Time-independent Schrödinger Equation

　For light wave function

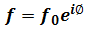
　Fermat Principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. The shortest path can be corresponded to the shortest path of phase .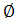

【Pierre de Fermat（1601－1665）】

　Principle of Least Action of Newtonian Mechanics is

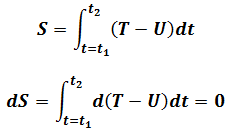
　For light wave of shortest path of phase, we can guess

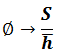
　Where 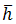 is Planck Constant over 2π. Because  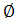is non-dimensional, we divide S by  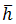for dimensionless.

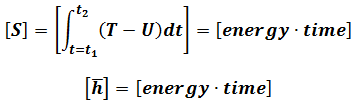
　So light wave function can become

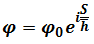
　For 1-dimension space, returning to

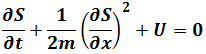
　With

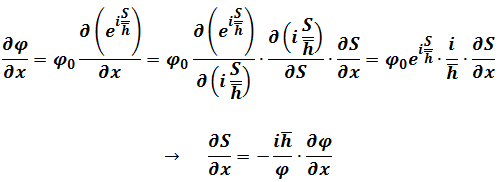
　For Hamiltonian Energy

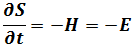
　So

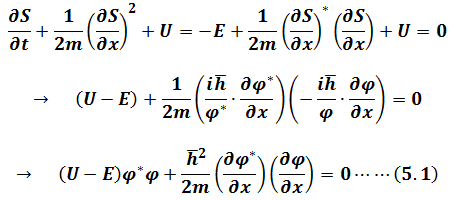
　To find the solutions of（5.1）which are the functions for which a given functional is stationary, let

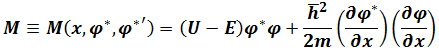
　Taking into Euler-Lagrange Equation

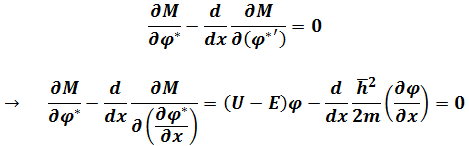
【Leonhard Euler（1707－1783）】

　Here we get

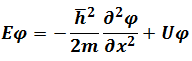
　This is Time-independent Schrödinger Equation.

Chapter 6－Derivation of Time-dependent Schrödinger Equation

　Huygens Principle proposed that every point which a light wave disturbance reaches becomes a source of a spherical wave. The sum of these secondary waves determines the form of the wave at any subsequent time.

【Christiaan Huygens（1629－1695）】

　For 1-dimension space, Feynman guesses

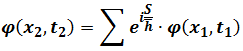
【Richard Feynman（1918－1988）】

　Using integral by summation

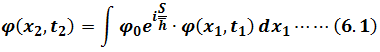
　If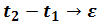 

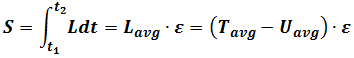
　Where

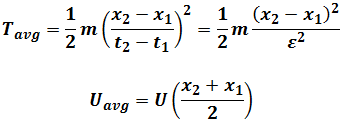
　We get

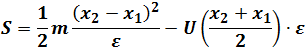
　So

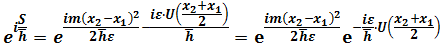
　Taking into power series about

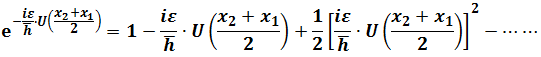
　Because 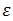 is very small and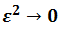 

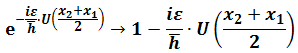
　（6.1）becomes

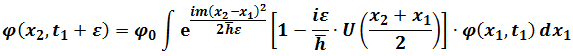
　Let 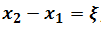, then  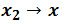and 

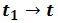
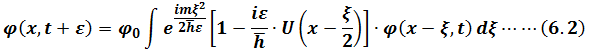
　Here using Taylor expansion

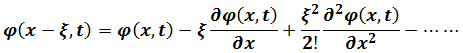
　is very small, so（6.2）becomes

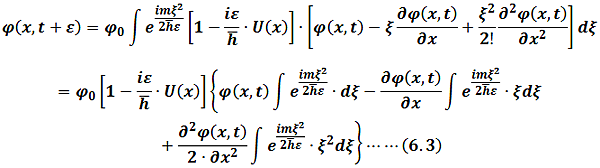
　According to Gaussian integral formula

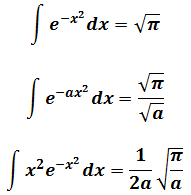
　With

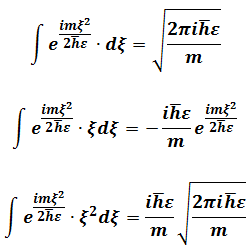
　（6.3）goes to

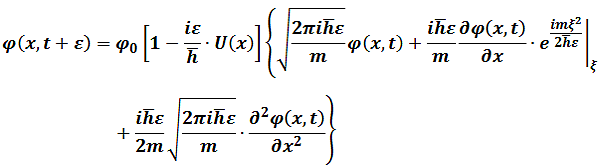
　Taking into power series and 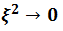 for

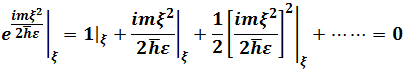
　So

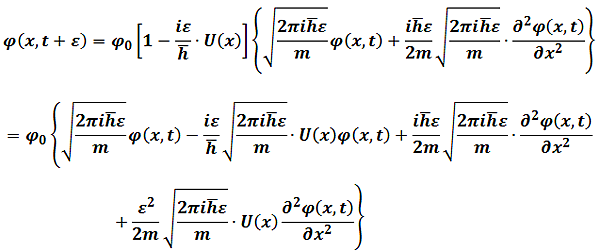
　And 

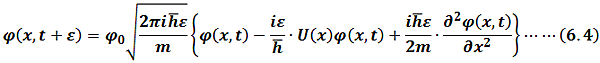
　For normalization constant, we can choose

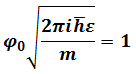
　So（6.4）becomes

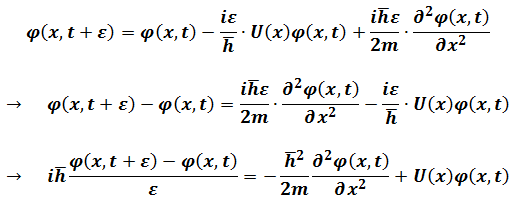
　Here we get

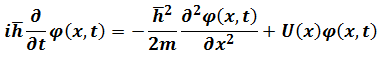
　This is Time-dependent Schrödinger Equation.