進動(Precession)為作旋轉運動之物體其旋轉軸又繞著另一軸旋轉的現象,如原地打轉的陀螺若稍有偏斜,它的「自轉軸」也會開始旋轉擺動。在太陽系中,行星繞著太陽公轉也是一種旋轉運動,公轉軌道呈現一橢圓軌跡,但實際上此公轉軌道並非固定,其橢圓亦會「旋轉」而形成進動。當行星和太陽最接近時稱為「近日點」,因為橢圓公轉軌道的旋轉,於是也有「行星近日點進動」的現象產生。由古典牛頓力學分析,造成行星近日點進動最主要是受到其他行星引力的拉扯,這是很理所當然的原因。另外,太陽的扁橢球體形狀也會產生太陽引力的不對稱,但這對行星近日點進動的影響是微乎其微。
【地球繞太陽公轉軌道之進動】
十六世紀之後隨著觀測技術的發展進步及天文學家的努力不懈,天文學界留下了大量又準確的觀測數據。西元1859年,法國天文學家勒維耶(Urbain Le Verrier,海王星的預言者)分析了從1697~1848年水星凌日的時間記錄,發現並計算出水星近日點進動的觀測值,比由古典牛頓力學算得的理論值,每一百年相差了38弧秒。1882年,加拿大天文學家紐康(Simon Newcomb)重新測定水星近日點進動率偏差值為每世紀43弧秒。
【水星近日點進動】
每世紀43弧秒,雖然此值微小到三百萬年後水星近日點才會進動一整圈,但科學家為了尋求這一偏差的解釋卻帶來更多的問題,如假想一顆未被發現的水內行星,甚至對牛頓重力定律提出根本性懷疑。直到西元1905年,愛因斯坦提出狹義相對論,光速的極限揭示古典牛頓力學在大天體尺度下的矛盾,然後廣義相對論的架構逐步建立,愛因斯坦開始思考自1859年以來一直困擾天文學家的「水星近日點進動」問題,並在1915年發表《用廣義相對論解釋水星近日點運動(Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie)》,計算了水星近日點的進動率偏差。
【彎曲時空中的公轉軌道示意圖】
根據廣義相對論,大質量的物體造成周圍的「時空」彎曲,而太陽的巨大質量也會造成時空彎曲,行星於是陷入了彎曲時空幾何中的公轉軌道,此即為引力的真正內涵。由愛因斯坦重力場方程式,當我們知道物質與能量在時空中如何分布,就能計算時空的曲率,然後利用測地線方程式求得物體在重力場中的運動軌跡。通過計算,愛因斯坦得出的水星近日點恰好是以每世紀43弧秒的速率在進動,符合觀測值的結果成為廣義相對論最有力的驗證之一。
因為彎曲時空中的公轉軌道並非真正的橢圓,所以行星的軌跡會隨著時間緩慢進動,廣義相對論的推導如下。在任何慣性系下觀測到的守恆量為兩點間的時空間隔,這個間隔被稱作原時τ,在四維正交座標系中其相對論不變量為:

太陽與行星公轉軌道運動,對應著一不帶電荷和角動量之球對稱質量M的重力場,愛因斯坦場方程式解的最簡單形式為史瓦西度規(Schwarzschild Metric),其相對論不變量:

史瓦西度規由德國物理學家史瓦西(Karl Schwarzschild)於西元1915年推導出,可利用測地線方程式的定義,給出四維球座標系的最短曲面路徑,可知時空產生了彎曲。
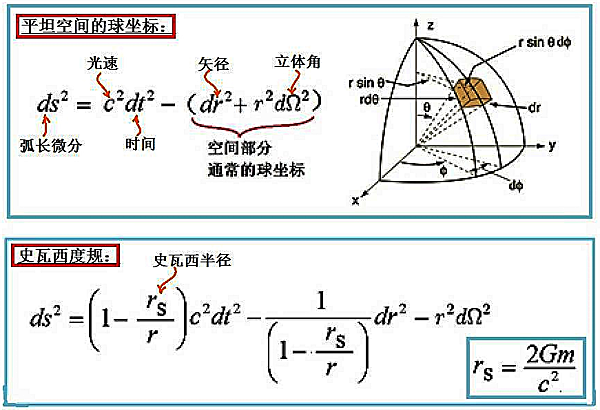
對行星軌道系統,任一θ皆可視為視角轉換的對稱,故可排除參數θ簡化史瓦西度規:

導出軌道運動的軌跡方程式:

其中,由重力場之能量守恆和角動量守恆,可令

所以得到不變量

代入整理可得軌道運動方程式


此即為能量與動能、位能關係式,可定義等效位能:

上式中,第一項是牛頓重力位能,第二項是具有排斥效應的離心位能,皆為古典橢圓運動力學的結論,而第三項僅在廣義相對論中才有導得,代表與距離立方成反比的吸引位能,此即為行星近日點進動的來源。由:

繼續換求軌道運動之極角方程式:

軌道運動方程式轉換成極角參數,可單純討論其旋轉運動軌跡對幅角的變化,並解出方程式的解。其中,先有參數變換的技巧,可令:

然後對U微分

其中有微分鏈鎖率

此即為行星軌道運動之極角方程式:

求解,令

極角方程式右邊第一項應對U0為古典力學的解(克卜勒第一定律),為不作進動完整封閉的橢圓軌跡:

極角方程式右邊第二項應對U1為廣義相對論中有關於吸引位能的解,可利用U0得到近似解法如下:

其中有三角函數倍角公式

接著,要用猜解法求微分方程的解。猜U1之形式為:

所以

比較係數得:

解出

所以,由廣義相對論推導出之行星軌道運動之極角方程式的全解為:

觀察上式。因為在行星軌道運動中:

故可忽略含有該係數之項,但為了要求得該運動極細微之角度變化,於是要保留為:

整理

其中有三角函數極限值

以及三角函數和角公式


【行星軌道近似橢圓的進動軌跡】
觀察廣義相對論導出之行星軌道運動之極角方程式的解,可發現其軌跡雖近似橢圓但確實不是橢圓,因Cosine項中極角函數產生了微小變化:

由此可得到行星運動軌道的週期角大於2π,於是造成行星公轉軌道的進動:

其中

即為行星運動軌道的進動率。考慮行星運動軌道為橢圓時:

近日點有

所以

代入得行星近日點進動率公式:

其中

對水星:

計算廣義相對論水星近日點進動率為(須注意單位換算):


此理論計算值幾乎同等於每世紀43弧秒的觀測值了!對太陽系中的其他行星而言,雖然皆會有廣義相對論之近日點進動,但它們的進動率相較水星實在是又太小了,幾乎更難察覺,所以水星近日點進動的觀測才會成為驗證廣義相對論的關鍵證據。








 留言列表
留言列表