 高談闊論狹義相對論
高談闊論狹義相對論 之後……
之後……
Question:我被那兩個方程式給卡到定格,伽利略跟勞倫茲……我不太了解物理歷史和它出現的時空背景,為何忽然天外飛來一律?又是如何被理解和應用?後來YOUTUBE了伽利略變換,就比較可以理解那個xyz的實際想像:「A和B兩人,8:00的時候原本在同一點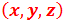 ,後來B走直線回家,5分鐘後到達
,後來B走直線回家,5分鐘後到達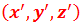 ,如果在8:05時發生了一件事,這件事跟B的距離是
,如果在8:05時發生了一件事,這件事跟B的距離是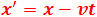 。」以上的數值和運動都是相對的,但只有時間是絕對的,不因A和B在不同坐標系而有不同,但我還沒進展到勞倫茲那更大塊的方程式……
。」以上的數值和運動都是相對的,但只有時間是絕對的,不因A和B在不同坐標系而有不同,但我還沒進展到勞倫茲那更大塊的方程式……
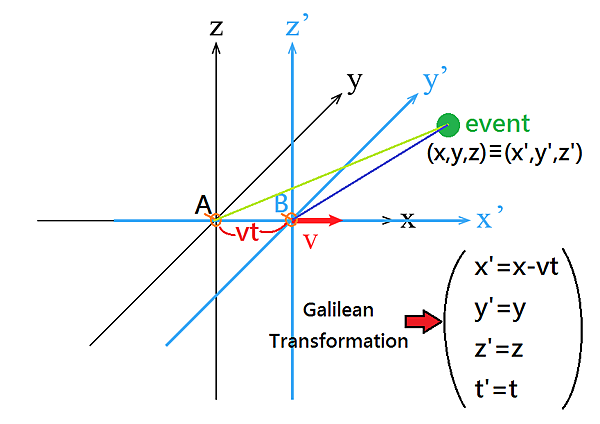
【伽利略變換示意圖】
以上關於伽利略變換(Galilean Transformation)的理解,仍落入了「單一座標系思維」的圈套,誤解之處在於 與
與 並非是同一座標系中,而是不同座標系的定位表達,表示了兩個不同參考座標系的相對轉換關係,所以才有「變換(Transformation)」之名。
並非是同一座標系中,而是不同座標系的定位表達,表示了兩個不同參考座標系的相對轉換關係,所以才有「變換(Transformation)」之名。
對伽利略變換的理解,可以重新修正敘述為:如上圖所示,8:00的時後A和B兩人在同一點,後來A不動,B沿正x軸方向、以速度v走直線回家,所以B和A之間的距離為一隨時間改變的參數「 」,此即為兩個參考座標系S(A)與S’(B)原點的距離。B走了5分鐘後(8:05),如果發生了一件事(event)跟A的距離為
」,此即為兩個參考座標系S(A)與S’(B)原點的距離。B走了5分鐘後(8:05),如果發生了一件事(event)跟A的距離為 ,那麼這件事跟B的距離就是
,那麼這件事跟B的距離就是 ,其中x與x’的變換關係式即為
,其中x與x’的變換關係式即為 。
。
在古典力學中,伽利略變換是用來轉換不同座標系對相同事件的定位描述,因為彼此以等速相對運動、參考原點不同(如A和B所看到),所以在不同座標系中觀察同一事件時,就會有不同表像,此乃「相對性原理」,也是牛頓第一運動定律「慣性定律」的基石。
科學巨人:伽利略

【伽利略,現代科學之父】
義大利人伽利略(Galileo Galilei;西元1564~1642年)身為當代的物理學家、數學家、天文學家及哲學家,展現了天才與博學,被譽為「現代科學之父」。歸納伽利略的重大成就有:
 改良天文望遠鏡,使天文觀測的技術大進步,驗證了哥白尼的日心說並引導克卜勒發現行星運動定律。
改良天文望遠鏡,使天文觀測的技術大進步,驗證了哥白尼的日心說並引導克卜勒發現行星運動定律。
 設計斜面滾球實驗,論證物體只要不受外力作用,就會保持原來的靜止狀態或等速運動狀態,此即為「慣性原理」,亦為牛頓力學的基礎。
設計斜面滾球實驗,論證物體只要不受外力作用,就會保持原來的靜止狀態或等速運動狀態,此即為「慣性原理」,亦為牛頓力學的基礎。
 設計有名的「比薩斜塔」落體實驗,發現落體運動非為等速運動而是加速度運動,證明落體的質量與落地時間無關,並啟發了牛頓發現萬有引力。
設計有名的「比薩斜塔」落體實驗,發現落體運動非為等速運動而是加速度運動,證明落體的質量與落地時間無關,並啟發了牛頓發現萬有引力。

【伽利略的斜面滾球實驗】
伽利略本來把等速運動叫做「均勻的移動」,但這樣定義是有瑕疵的,因為描述物體運動除了「速度」之外,還得要說明「方向性」。以圓周運動為例,若只知道速度卻不說明「向心」,我們將認為該物體是在做直線運動。後來,牛頓(Isaac Newton;西元1643~1727年)指出運動的方向性並加上「直線」條件,才建立了「牛頓三大運動定律」。

【牛頓說:我站在巨人的肩膀上】
牛頓曾說:「If I have seen further, it is by standing on the shoulders of giants.」伽利略對「速度」本質的研究,架構了「相對性原理」與「伽利略變換」的基礎,並啟發牛頓力學。伽利略是科學革命的巨人,他的成就造成十六世紀歐陸的科學躍進,影響物理學發展深遠。
勞倫茲變換的推導
相對性原理是普遍的物理定律,但狹義相對論引進了「光速恆定」假設,使得古典的伽利略變換修正為「勞倫茲變換(Lorentz Transformation)」。推導勞倫茲變換之前,先從伽利略變換開始:

但狹義相對論闡述的是空間、時間與速度的「相對性」,若以伽利略變換為出發點,在S座標系,我們可以重新假設空間x與x’的變換關係式為:

其中γ為一未知參數,新的變換形式表現空間、時間與速度的「相對性關聯」。當然,我們也可以在另一個參考座標系S’來作相對變換:

現在考慮「光速恆定」的假設。在不同參考座標系中,我們觀察到的真空光速始終恆為定值c,所以光在S 與S’座標系的運動距離分別為 與
與 ,代入(1)與(2)式整理可得:
,代入(1)與(2)式整理可得:


把t’代入t:

兩邊消去t並移項合併:

γ推導出來了!於是空間x的勞倫茲變換式就能寫成:

我們也能求時間t的變換式。由(2)式可整理得:


代入 可求時間t的勞倫茲變換式:
可求時間t的勞倫茲變換式:

以上即為勞倫茲變換的數學推導。最後,我們得到空間與時間的勞倫茲變換總式,可發現時間不是絕對的:

 相關主題請參閱誰來對我高談闊論「狹義相對論」
相關主題請參閱誰來對我高談闊論「狹義相對論」





 留言列表
留言列表