感覺Brouwer's fixed point theorem @ 阿衡的探秘地圖

　　Brouwer's fixed point theorem的描述為：對於一個拓樸空間中滿足一定條件的連續函數f，存在一個點 $x$ $0$ ，使得f( $x$ $0$ )＝ $x$ $0$ 。簡單來說，若有一實數代數方程式f(X)＝y＝ax＋b，則存在fixed point $x$ $0$ 使得y＝ $x$ $0$ ＝a $x$ $0$ ＋b。在線性代數中這似乎是一個顯而易見的定理，然而若應用在其他拓樸空間中的情形是怎樣呢？

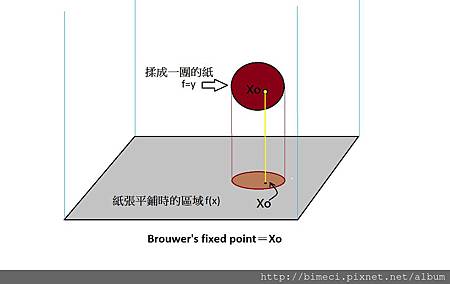
　　似乎很抽象，不過或許可以這樣想像：將一張Ａ４紙平鋪在桌面上，再把紙揉成一團，放在原來紙張所在的地方，只要紙團放置的範圍不超出原來紙張平鋪時的邊界，那麼被揉成一團的紙團中一定有一個點 $x$ $0$ ，而 $x$ $0$ 垂直在桌面上的投影點，會與原來在紙張平鋪時 $x$ $0$ 所在的位置是重合的。等效對應到線性代數的例子，紙上的平面為所有x的集合，揉成一團的動作則可視為滿足一定條件的連續函數f＝y（所以揉的時候不能撕破紙），而投影點fixed point即為 $x$ $0$ 。

　　關於紙張情況的Brouwer's fixed point theorem證明，以數學界的術語和論證方式完全一竅不通（或許念數學的朋友有空來指教一下）……但我想或許可以用逼近的方法去做做看。

　　假設一個完美的情形：Ａ４紙被揉成一團完美的球型，放在不超出原來平鋪時的邊界內，在正上方射入垂直方向的光線，則完美紙球會在原來平鋪的紙張上，映射出一個投影圓。接著拿支筆把投影圓的邊界做記號描出來，然後把紙球展開成原來的Ａ４紙張，再比對記號，在紙上該處把投影圓畫出來。

　　我們可以直覺認為，紙球中對應到這個投影圓集合的垂直投影，必然包含在該投影圓上，造成一種「fixed zone」的狀況。因此對於紙球中「對應到這個fixed zone外的集合」，我們可以拿剪刀沿著之前畫好的圓把它「剪掉」，原來的平鋪Ａ４紙面就會變成一個較小的投影圓紙面。然後再把圓紙揉成一團較小的完美紙球，放在不超出原來平鋪時的邊界內（這個邊界變成圓形的了），在正上方射入垂直方向的光線，則小紙球又會在原來平鋪的紙面上，映射出一個更小的投影圓，再拿剪刀剪掉對應到這個更小投影圓外的集合，再展開……如此繼續重覆下去，則投影圓會越來越小，最後逼近成一個點，直到不能再拿剪刀剪掉任何東西了，該點就成為我們所要求證的fixed point了。

　　然而，在每次的重複動作中，只要紙球放置的位置不超出原來平鋪時的邊界，則很直覺能去想像那個fixed point可以應對到紙上邊界內的任何地方，而fixed point的不同取決於紙球放置的位置差異而已。

　　反過來看，若存在「紙球中對應到這個投影圓的集合可以不包含在該投影圓上」的情況，則很明顯不可能成立，這就像是我們把紙球撕一塊出來丟在旁邊一樣，這違反了之前所定義的「連續函數」前提，也就是不能把紙撕破。

　　最後，再從完美球形推論到一般情形（隨便揉成任何形狀），甚至再推廣到其他維度的拓樸空間，因為本質不變，其證明我想只是技術上的問題而已了。

　　這個定理看起來很簡單，但再深入思考時，會發現它對於物理學中的座標系轉換成立與否，占有相當重要的本質性意義。我們只要找出（或規範）不同座標系之間的連續函數相互關係，fixed point就可使彼此之間的座標轉換是可行的！fixed point就是不同座標系之間的參考聯繫依據。如遊樂場中常看到的平面地圖，上面標示「你在這裡」的紅點，如果相關位置註明詳實，那麼這個紅點就是把遊樂場實際地形映射到平面地圖的fixed point。從以上簡單的日常生活例子，延伸到討論轉動物體的自轉軸、GPS定位，甚至是微分幾何、廣義相對論等等，可以瞭解到它們的根本都是由Brouwer's fixed point theorem所建立的。

學術資料與術語補充：

　　布勞威爾不動點定理（Brouwer's fixed point theorem）：對於一個拓樸空間中滿足一定條件的連續函數 $f$ ，存在一個點 $x$ $0$ ，使得 $f$ $(x 0) = x 0$ 。布勞威爾不動點定理最簡單的形式是對一個從某個圓盤 $D$ 射到它自身的函數 $f$ 。而更為廣義的定理則對於所有的從某個歐基理德空間的凸緊子集射到它自身的函數都成立。