Covariance and Contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. They are the mathematical foundation to understand General Relativity.

【James Joseph Sylvester(1814-1897)】
The terms Covariant and Contravariant were introduced by James Joseph Sylvester in 1853 to study algebraic invariant theory. Now they are extensive using in Tensor Field analysis of mathematics, physics, and engineering, even in General Relativity. In order to understand what Covariance and Contravariance are in a vector space, in the beginning, a vector can be written as
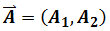
Define "Covariant" form
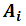
And "Contravariant" form
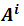
Now we can write "two forms" of the square of a vector
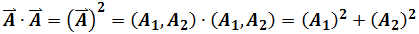
And
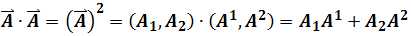
The square of a vector means square of itself length and it should be unchanged. The product of two vectors has "two forms"
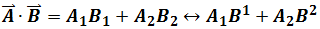
Covariant and Contravariant Vectors
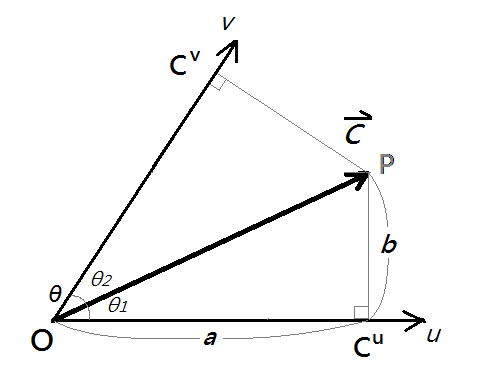
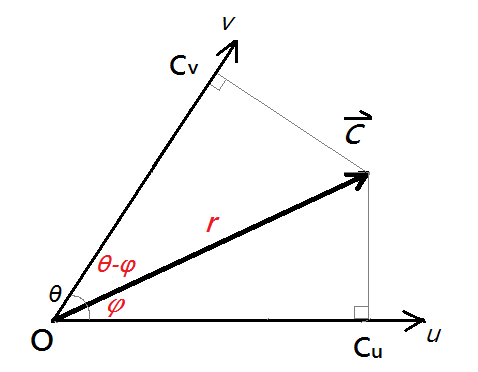
Considering a non-Cartesian coordinate system with non-orthogonal angle θ between u-axis and v-axis
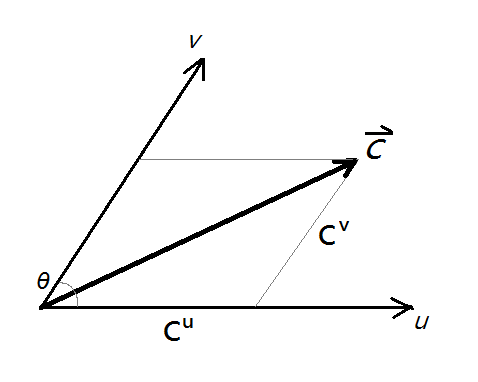
The vector C
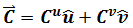
If we put the vector C back to Cartesian coordinate system
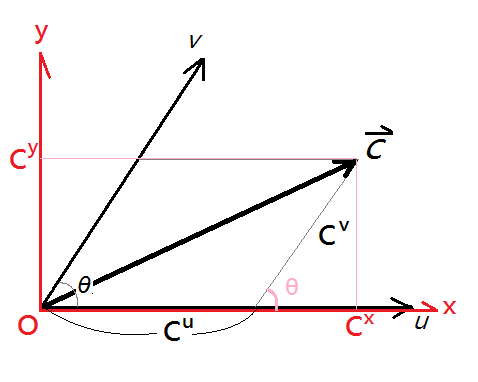
Where
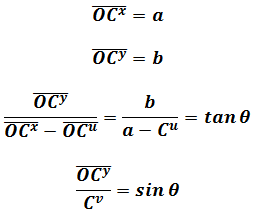
The transform from Cartesian coordinate system to this non-Cartesian one are

In matrix form
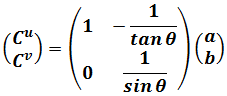
Now try to calculate the square of vector C. In Cartesian coordinate system
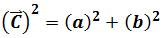
In this non-Cartesian coordinate system
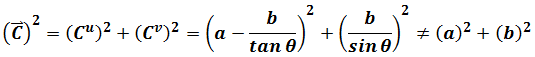
We find the square of vector C is “not” unchanged. It is a trouble to discuss physics problem in different coordinate systems.
Now try to another way. In this non-Cartesian coordinate system, we have
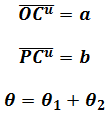
And
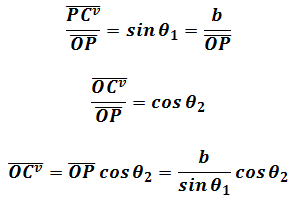
Where
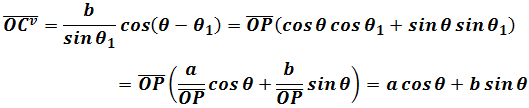
Then find the “orthogonal” components of vector C are
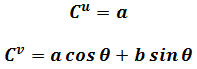
In matrix form
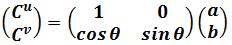
Again we calculate the square of vector C. In this non-Cartesian coordinate system, let contravariant components of vector C are
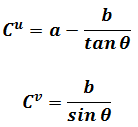
"Contravariant" means they are this non-Cartesian coordinate components transform into Cartesian coordinate system. Next, let covariant components of vector C are
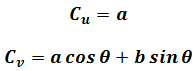
"Covariant" means they are this non-Cartesian coordinate's orthogonal components. Now
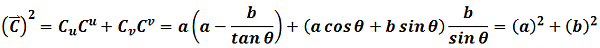
So we get the "invariant", the length of vector C is
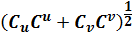
It must be unchanged in any coordinate system. Because of the invariant, that's why contravariance and covariance are particularly important for understanding how the coordinate description of a vector changes in passing from one coordinate system to another.
Example-Polar Coordinate System
The vector C
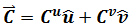
If we put the vector C back to polar coordinate system which is also orthogonal with its basis
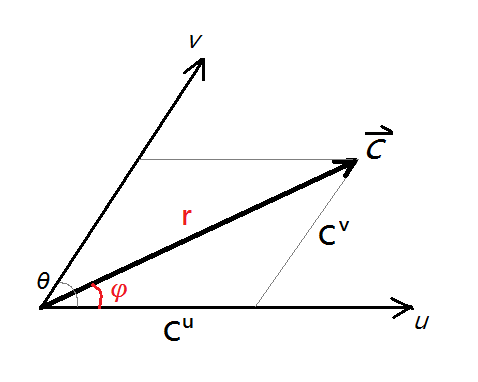
Law of sines
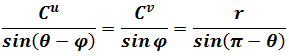
The contravariant components are
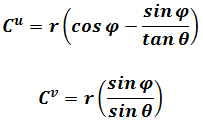
In this non-Cartesian coordinate system
The covariant components are
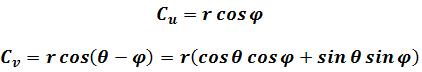
Then
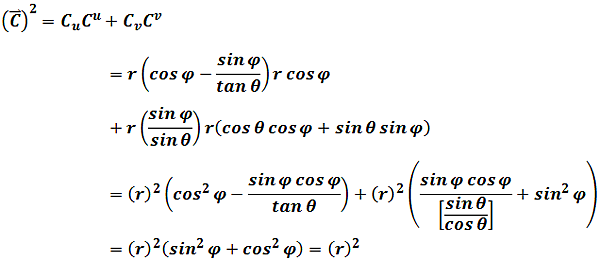
Again we get the "invariant" of vector C.
Einstein Summation Convention

【Albert Einstein-1920】
The method Using covariance and contravariance and adding up their products to get the invariant of vector in different coordinate systems is also known as Einstein Summation Convention or Einstein Notation. It was introduced to physics by Albert Einstein in 1916. He defined
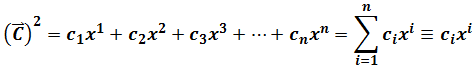
In General Relativity, upper formula means the invariant in any coordinate system transform. For Minkowski Space or Spacetime, the invariant of line element is
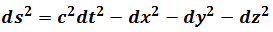





 留言列表
留言列表